
SRMR is a measure of approximate fit of the researcher’s model. Therefore, a cut-off value of 0.08 as proposed by Hu and Bentler (1999) appears to be more adequate for PLS path models. SRMR values of 0.06 and higher (Henseler et al., 2014). A recent simulation study shows that even entirely correctly specified model can yield A value of 0 for SRMR would indicate a perfect fit and generally, an SRMR value less than 0.05 indicates an acceptable fit(Byrne, 2008). the Euclideanĭistance between the two matrices. Standardized root mean square residual (SRMR) (Hu and Bentler, 1998, 1999)= the square root of the sum of the squared differences between the model-implied and the empirical correlation matrix, i.e. Currently, the only approximate model fit criterion implemented
There is more than one way to quantify the discrepancy between two matrices,įor instance the maximum likelihood discrepancy, the geodesic discrepancy dG, or the unweighted least squares discrepancy dULS (Dijkstra and Henseler, 2015a), and so there are several tests of model fit.Īpproximate model fit criteria help answer the question how substantial the discrepancy between the model-implied and the empirical correlation matrix is. Ones of the actual model, it is not that unlikely that the sample data stems from a population that functions according to the hypothesized model. If more than 5 percent (or a different percentage if an α-level different from 0.05 is chosen) of the bootstrap samples yield discrepancy values above the This modification entails an orthogonalization of all variables and a subsequent imposition of the model-implied Bootstrap samples are drawn from modified sample data. PLS path modeling’s tests of model fit rely on the bootstrap to determine the likelihood of obtaining a discrepancy between the empirical and the model-implied correlation matrix that is as high as the one obtainedįor the sample at hand if the hypothesized model was indeed correct (Dijkstra and Henseler, 2015a).

Saturation refers to the structural model, which means that in the saturated model all constructs correlate
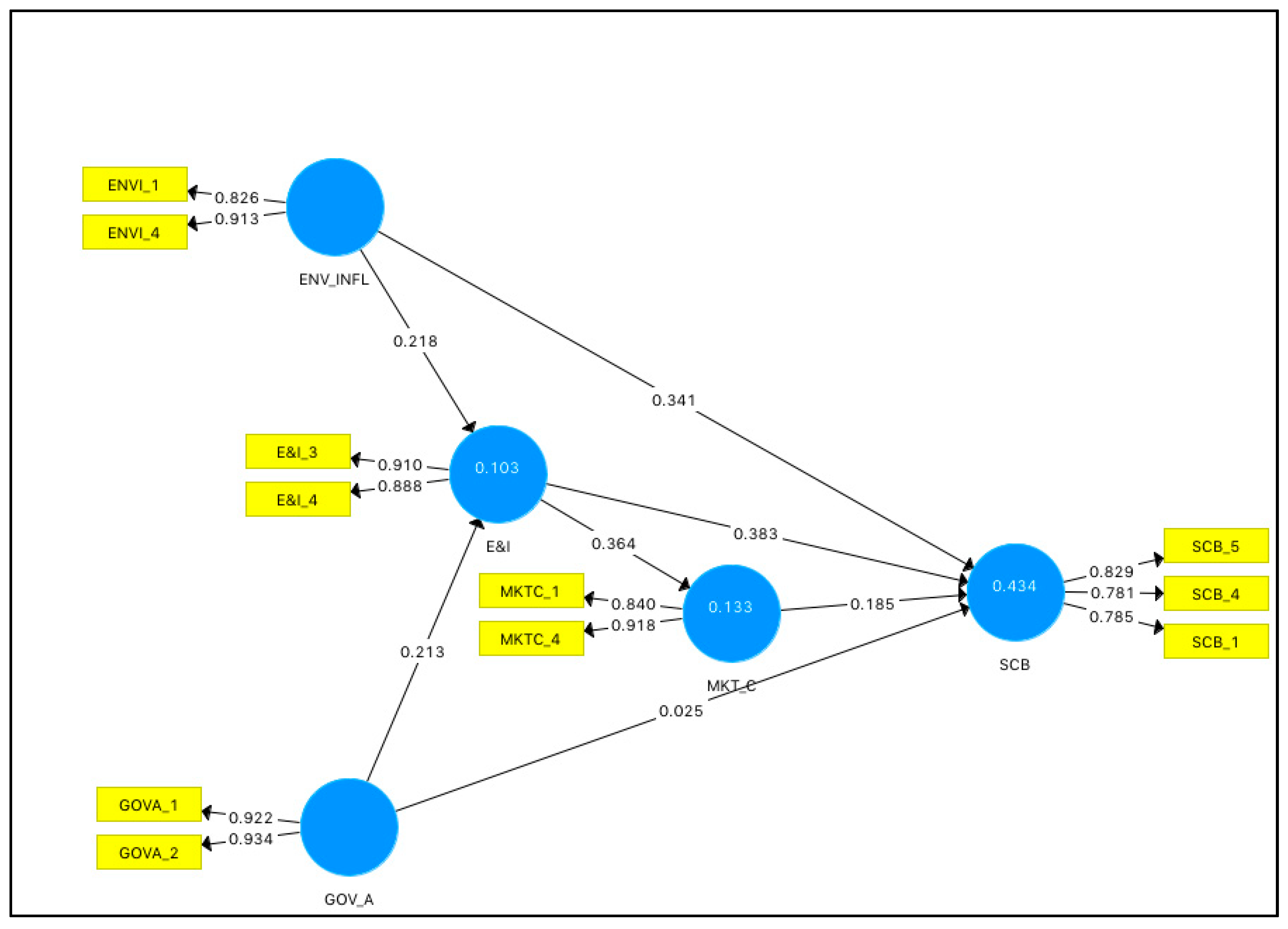
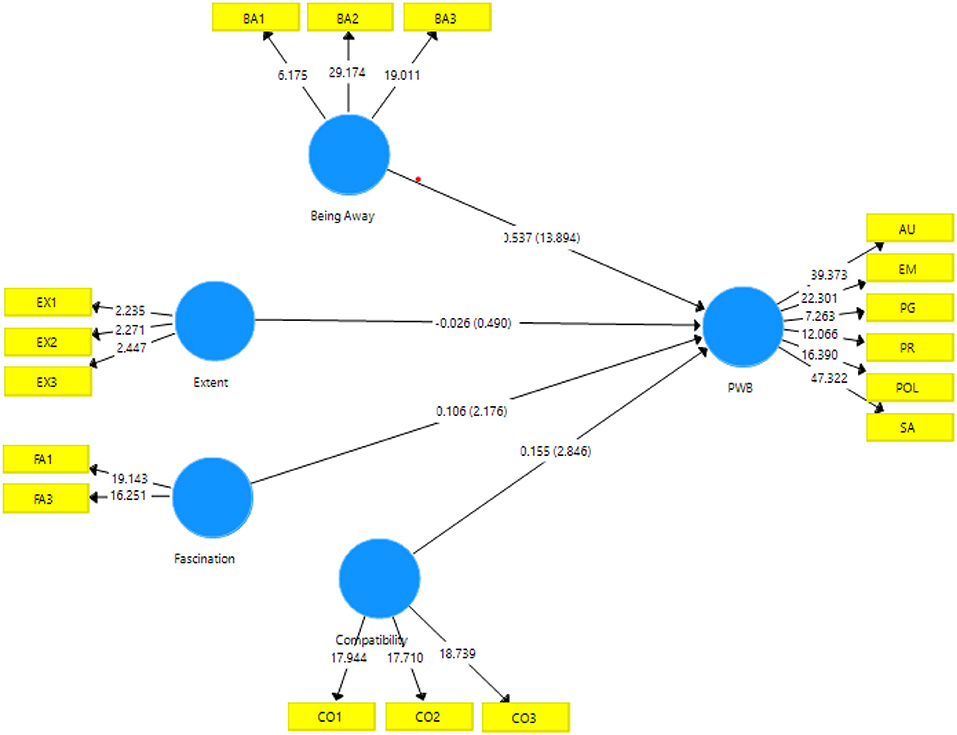
In order to have some frame of reference, it has become customary to determine the model fit both for the estimated model and for the saturated model. so-called tests of model fit, or through the use of fit indices, i.e. The global model fit can be assessed in two non-exclusive ways: by means of inference statistics, i.e.


 0 kommentar(er)
0 kommentar(er)
